Click-Wheel Organ

In high school I took a pile of rubber bands and foam board and built something vaguely resembling a guitar. It was impossible to tune, broke if you looked at it wrong, and launched a years-long obsession with instrument design that continues to date. Recently, I have been experimenting with different sound mechanisms, trying to tune anything that makes noise.

The range of sound mechanisms used in instruments is immense and much wider than I realized when I started, but a surprisingly large number of them can be made using PVC, wood, plastic bags, or tin-can reeds. Unfortunately, the gap between noise maker and musical instrument is wide, and my pile of out tune prototypes continued to grow. Nothing would stay in tune, until I started experimenting with click-wheels.

Instead of vibrating a delicate reed using air power, I could mechanically shove a reed up and down by pressing it against a toothed wheel. By cutting wheels with different numbers of teeth, different frequencies are able to be played. Despite being reliant on wheel speed for absolute tuning, the constant mechanical ratios between the notes guarantee that each note will stay in tune with each other, and thus be able to play music.

After my third prototype worked, playing a 6-note pentatonic scale, I knew I had to make one with a wide range. One weekend of laser cutting and gluing later, I had a working 3 octave instrument. Despite sounding like a swarm of musical bees, I was immensely excited to finally be able to play some real music.

As I have little patience working on anything remotely automatable, I wrote a Python script to automatically generate the wheels, converting a list of tooth counts and note names to a set of labeled, laser-ready polygons. As higher pitches are perceived as louder with the same amplitude, the larger wheels are cut with smaller teeth, equalizing the volume and allowing each wheel to have the same radius.

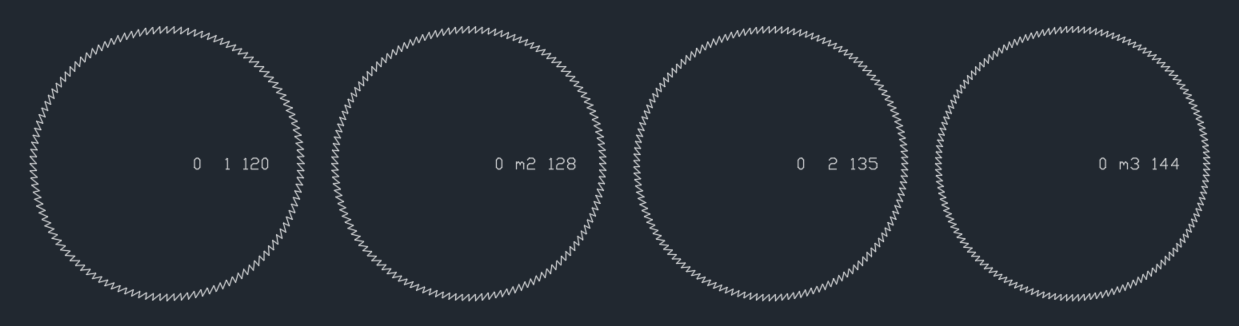
Another interesting problem was selecting a starting spike count. Each of the twelve notes in an octave has a specific ratio relating its frequency to the base frequency, but these are fractions. The spike counts must be whole numbers, as you can’t make a symmetrical wheel with an extra half spike. I decided to tune it to C, as just intonation has cleaner ratios, and started spreadsheeting. I wrote an error function for a given starting count, summing the difference between each ratio and it’s closest approximation, and got the following graph:

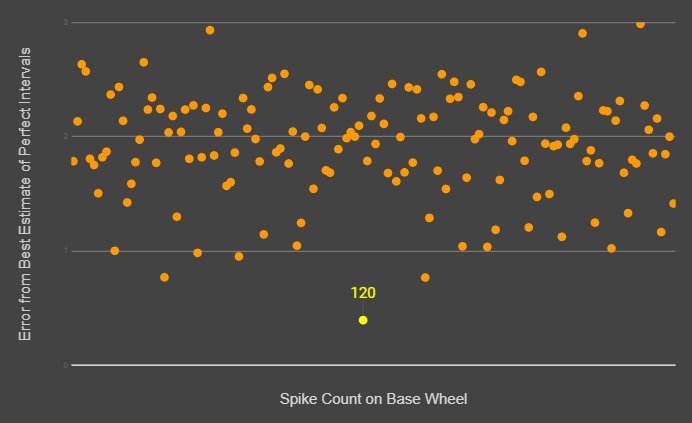
As you can see, 120 is a clear outlier. There are technically better approximations with much larger wheels, but 120 spikes strikes a lovely balance between size and accuracy. If anyone else is considering making a click-wheel organ, I would recommend using equal intervals instead to play in multiple keys. The following are my calculated spike counts for each note.

I’m unreasonably excited to complete my first original instrument. If anyone wants to build their own or take a close look, I’ve uploaded the CAD and code to Thingiverse . Feel free to shoot me an email if you have any questions or are building one for yourself!

EDIT:

This post was featured on the Hackaday Blog and Podcast !